On this page, we present audios and plots in order to illustrate our paper. We recommend you to wear headphones in order to hear all the subtleties.
Listening to the dataset
Here are 200 drum sounds from the dataset (the lengths of the audio are restricted from 21000 to 12000):
Unconditioned Generation via SDE discretization
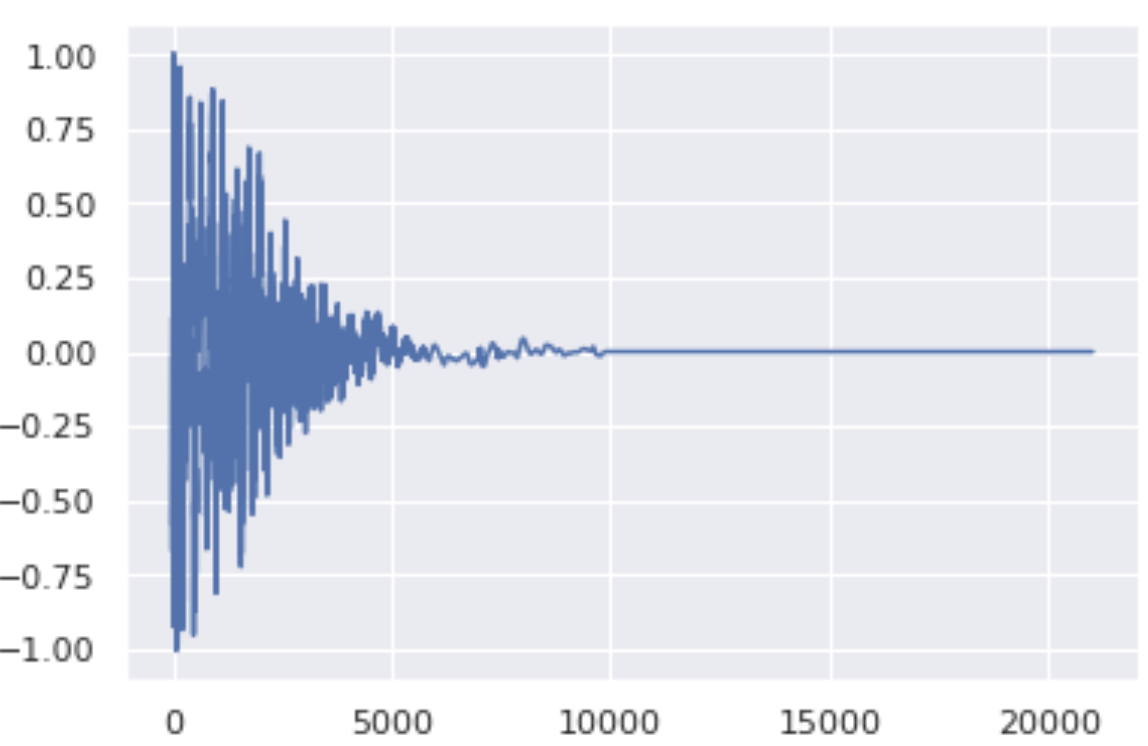
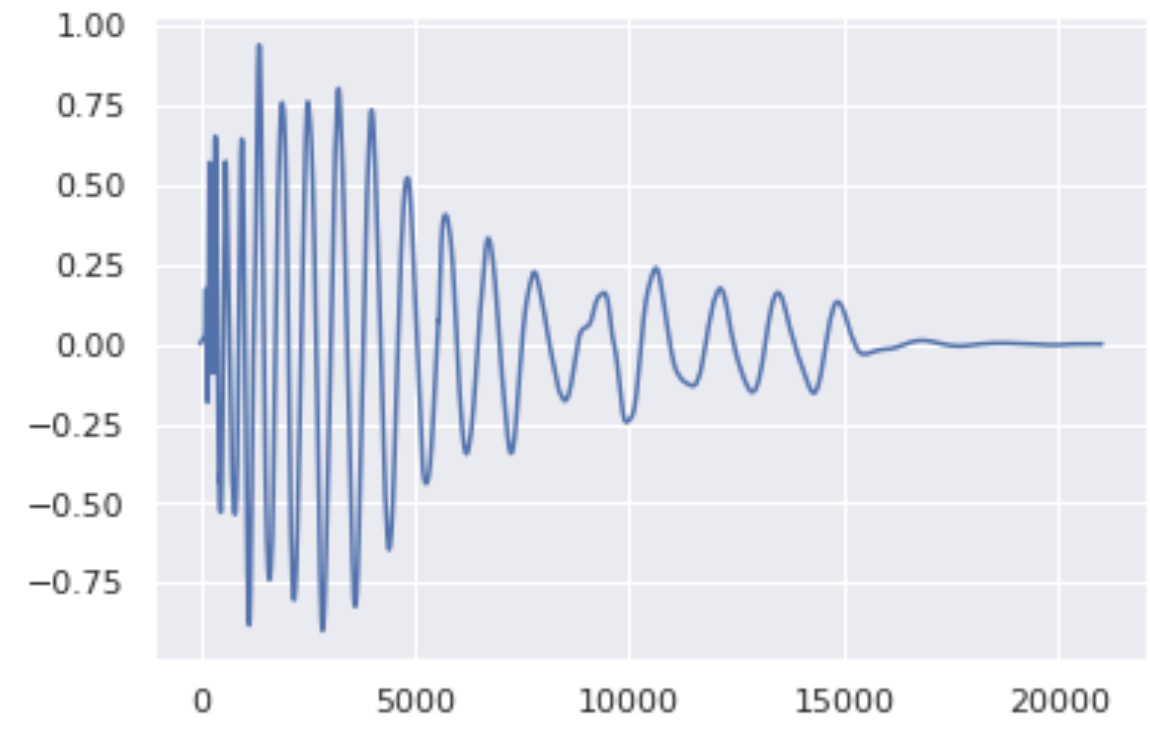
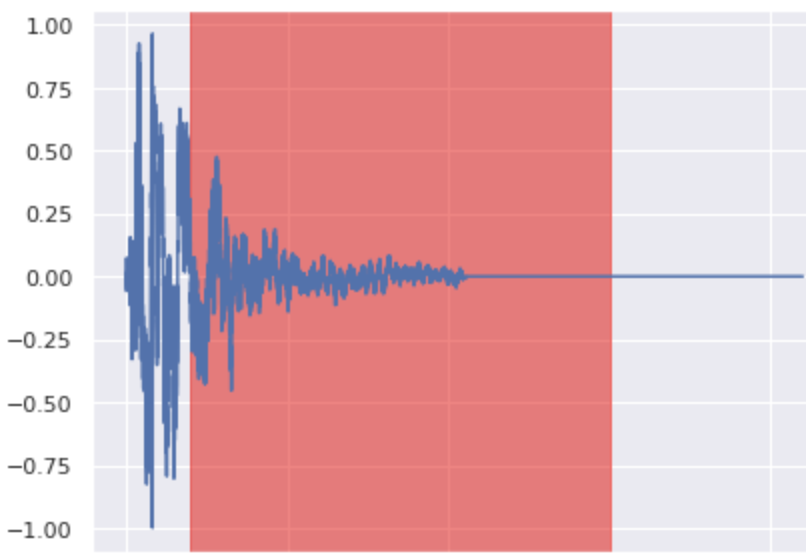
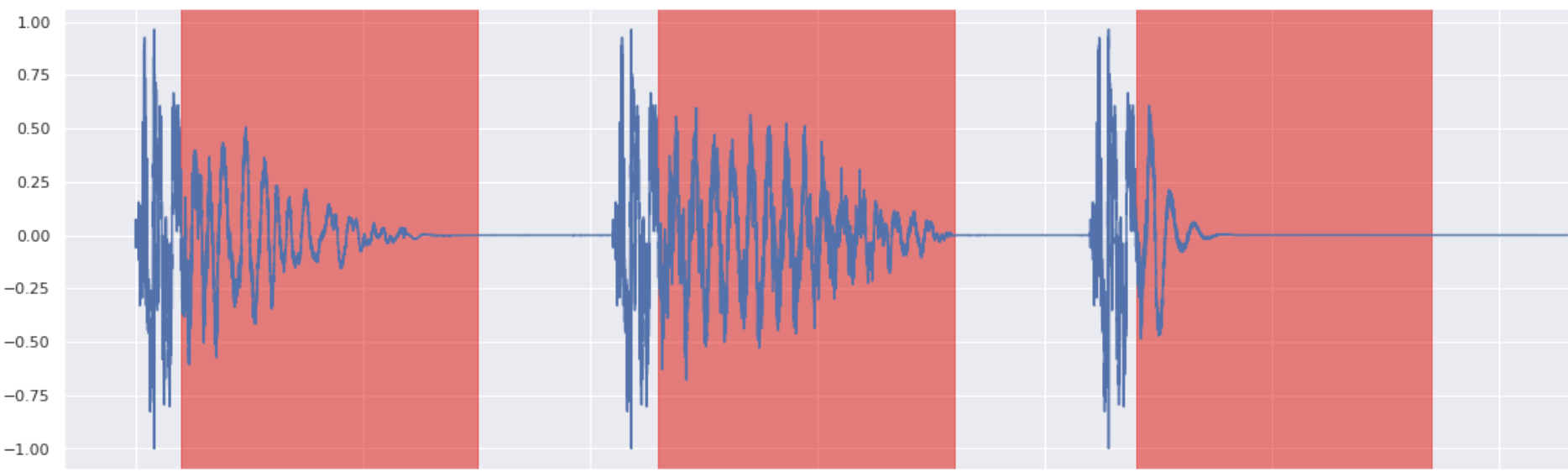
Here are 3 drum sounds (Snare, Kick and HiHat) with their waveform plots generated via discretization of SDE with 400 steps.
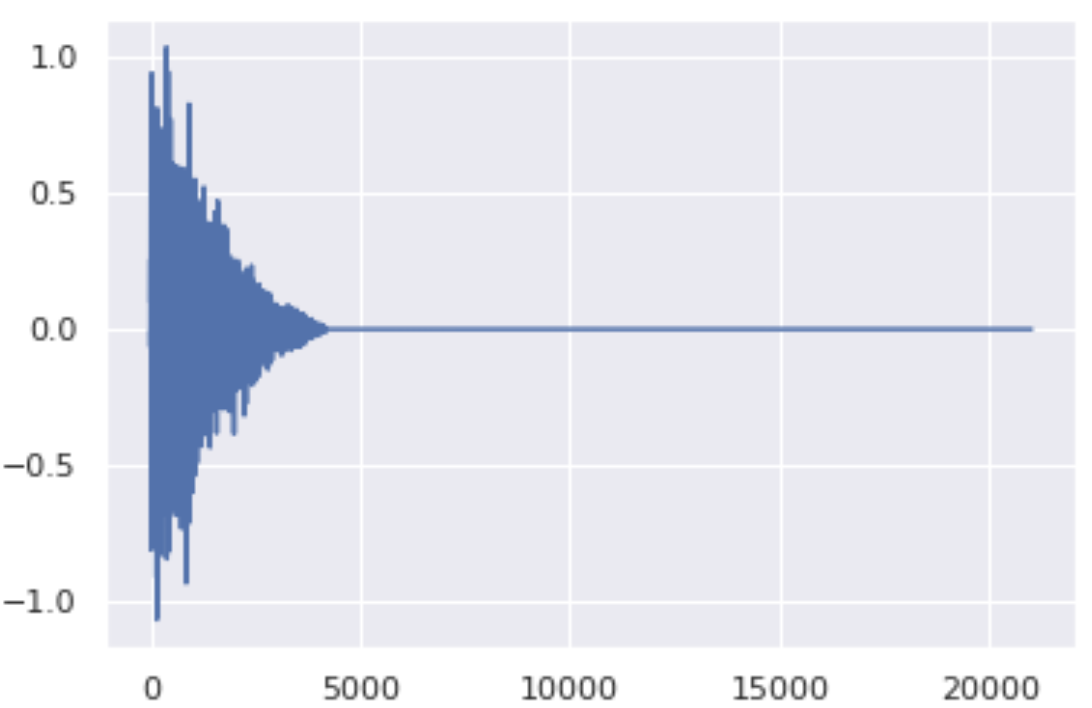
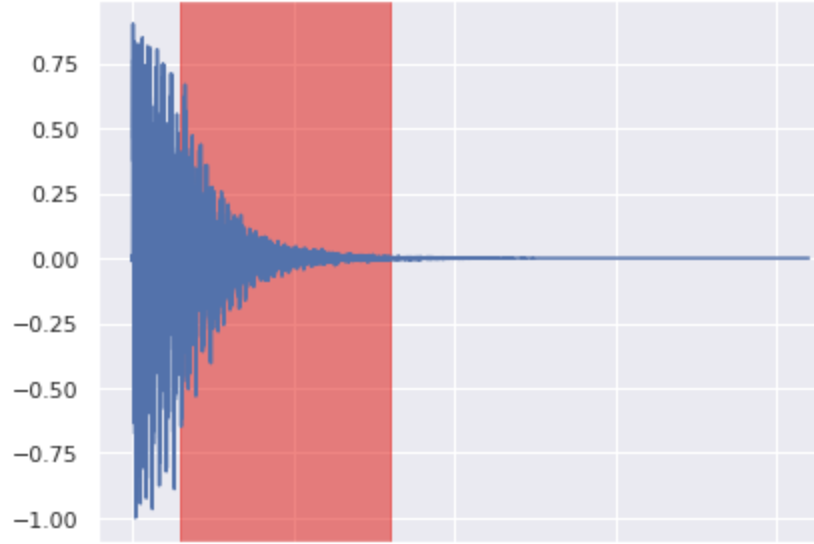
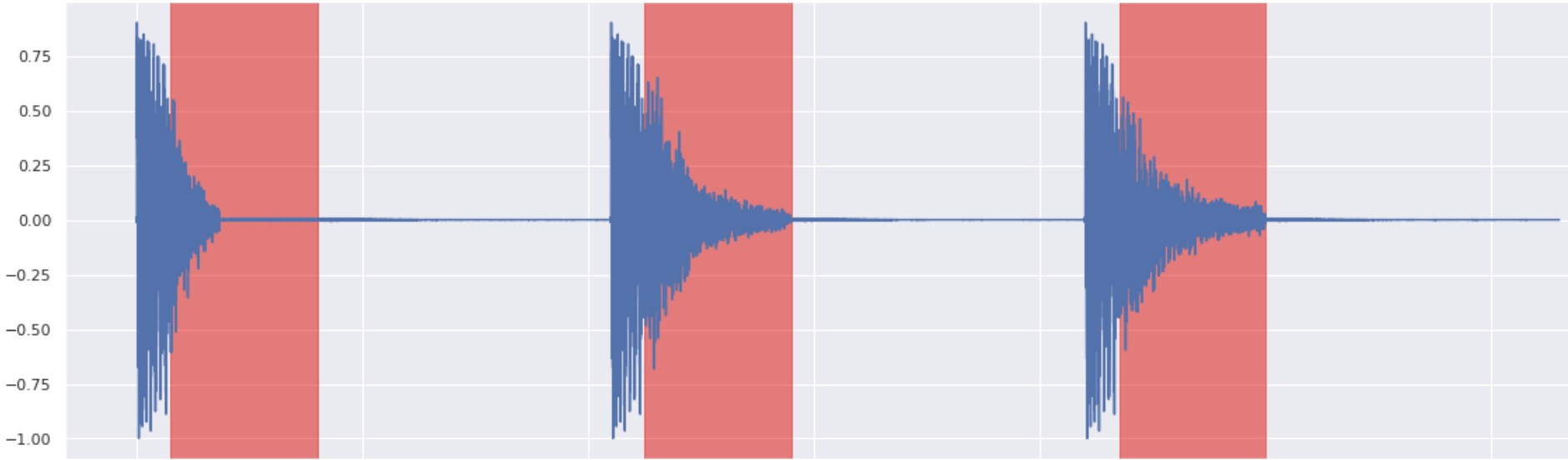
Here are 200 drum sounds generated via ODE discretization (sub-VP-1_1 schedule and 400 steps of discretization):
We note that the generated samples are less diverse than in the original dataset. This is not dramatic because the most interesting applications are in the domain of interactive sound design.
Interpolations in the latent space x(T) via ODE discretization
Here is a schema to explain the interpolation process:
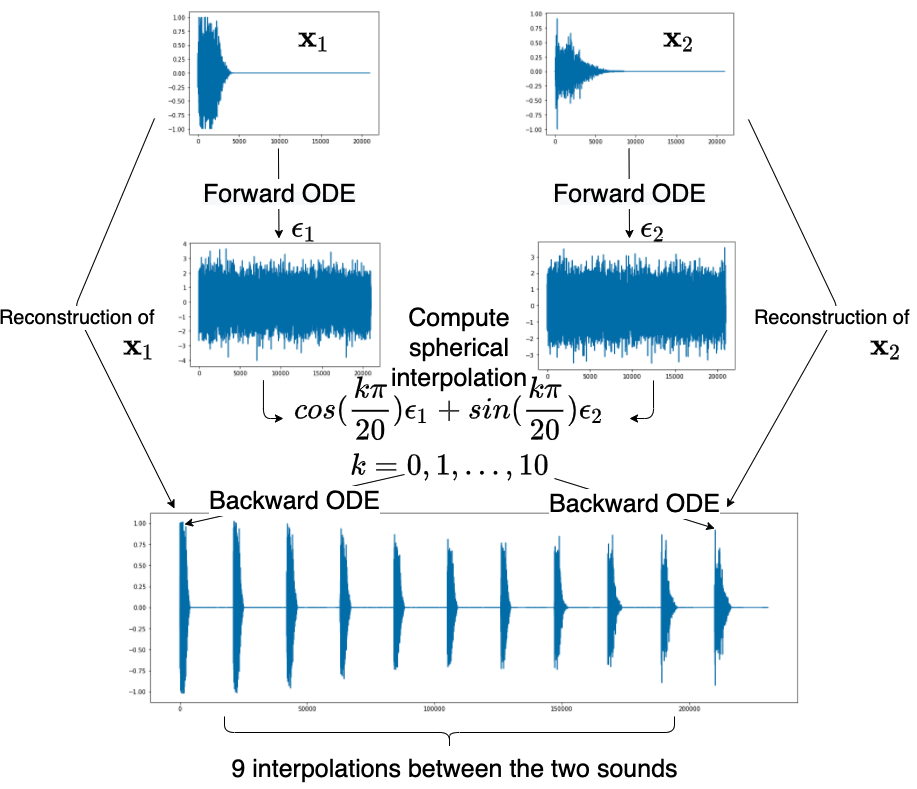
We provide the associated sounds:
The HiHat (x1): , The snare (x2):
The associated noises (be careful if you are wearing headphones, it might be loud!): ,
The interpolations (the first and the last one are the reconstruction of the 2 original sounds):
Click here if you want to hear the 11 sounds in a row:
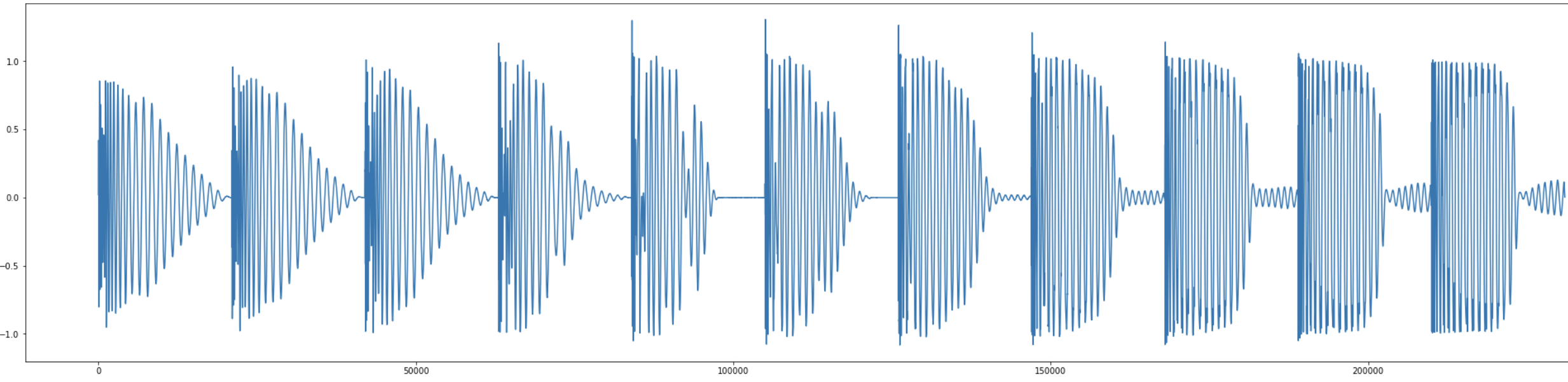
Second Interpolation
This is an interpolation between two kicks, you can see that the interpolation attenuates at different levels the “saturated vibration” of the second kick. Once again, we let you appreciate the quality of the reconstruction of the first and last sound.
Kick 1: , Kick 2:
Interpolations:
Click here if you want to hear the 11 sounds in a row:
Inpainting
Imagine that you don’t like a part of a drum sound, you can regenerate the desired part by fixing the part you like (readjusted with the accurate noise level at each step) during inference time. All the presented examples are from the test set. For each example, the first sound is the original sound and the following are inpainted versions.
Kick Inpainting 1
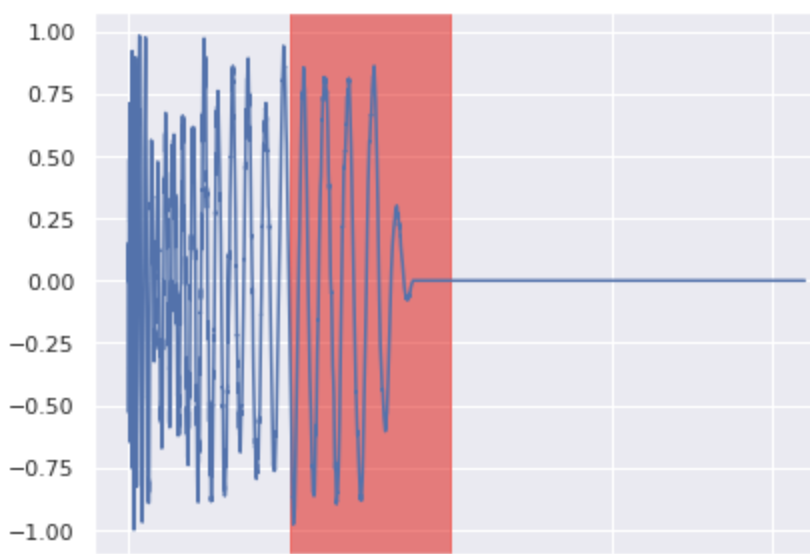
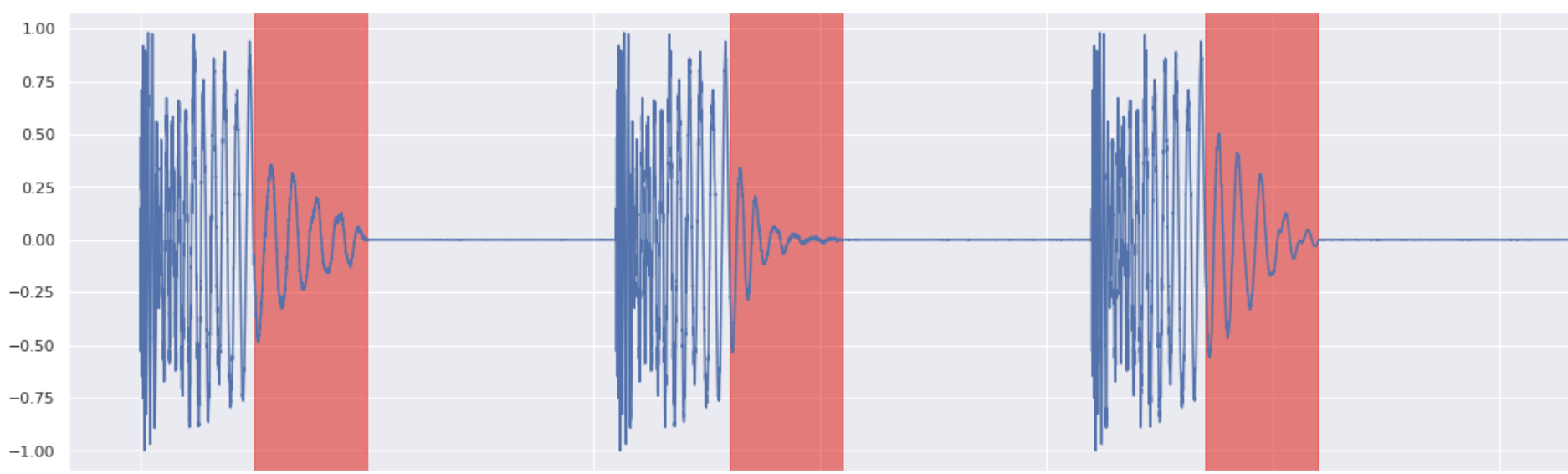
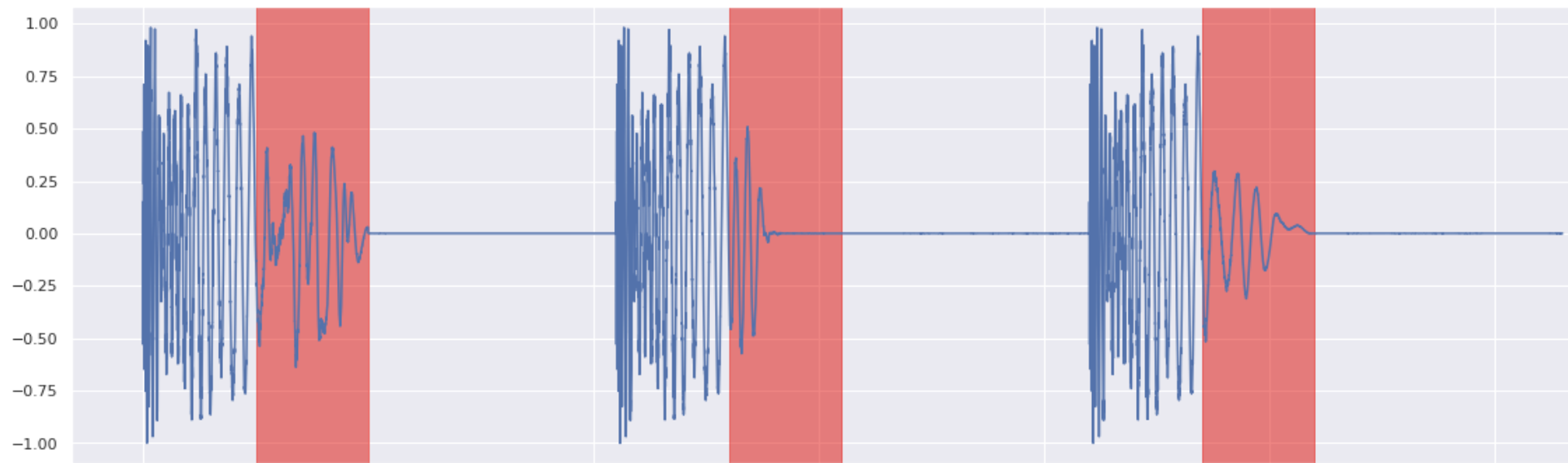
Kick Inpainting 2
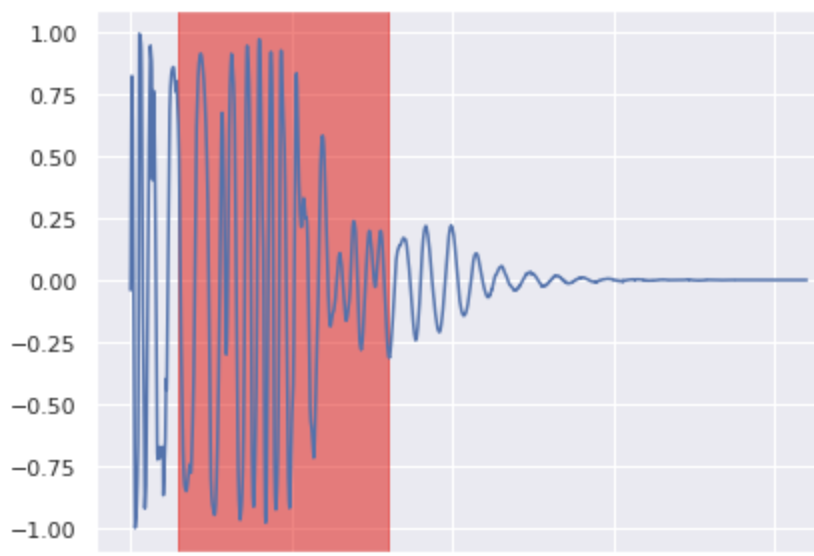
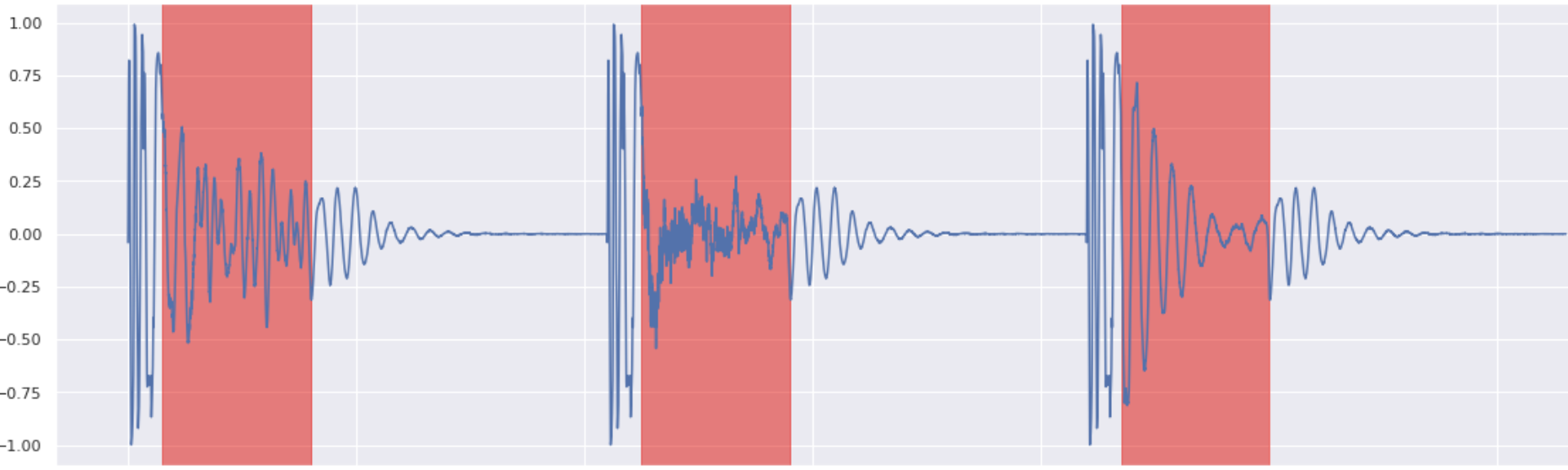
Kick Inpainting 3
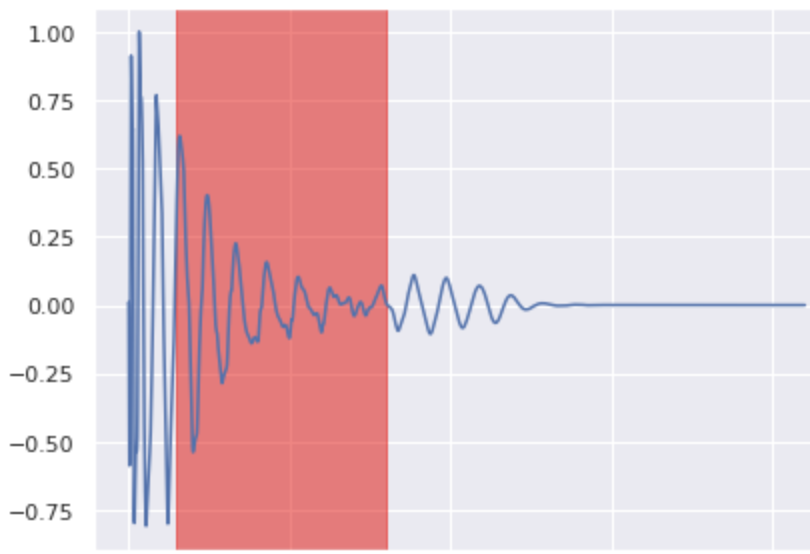
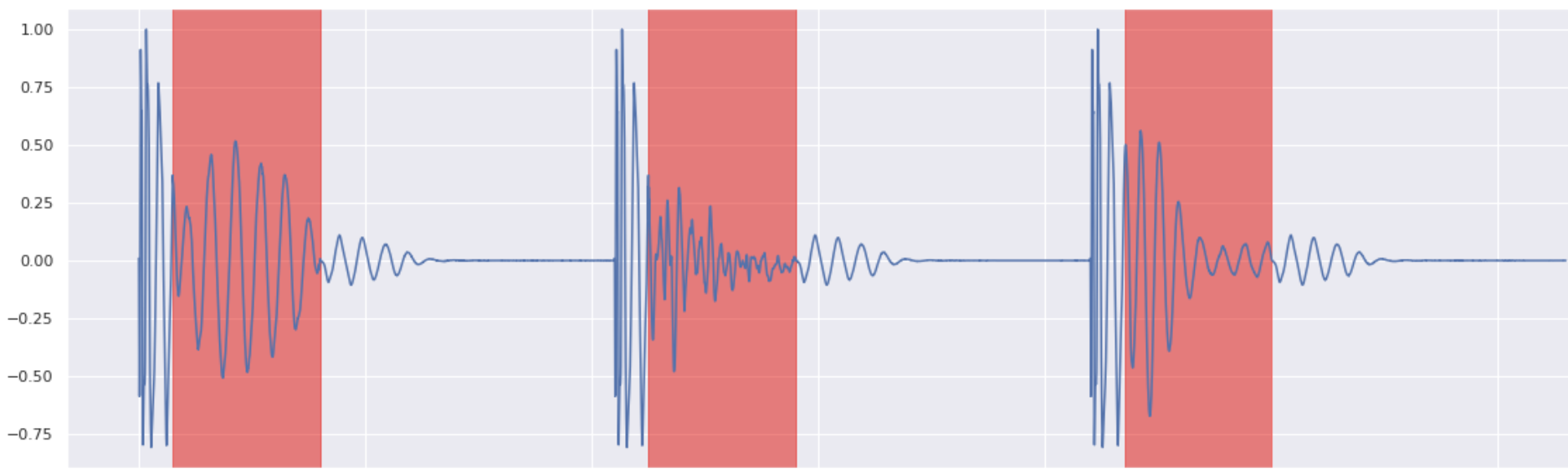
Kick Inpainting 4
Note that if the original waveform is thick, the generated part is also thick.
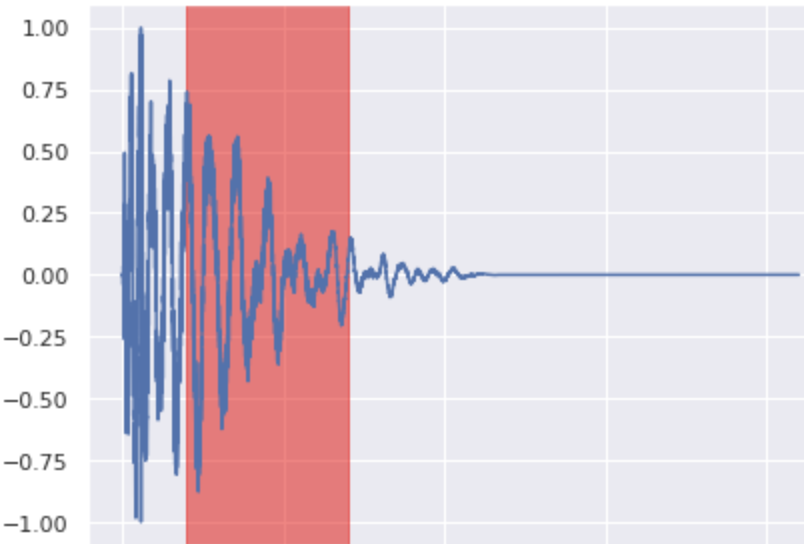
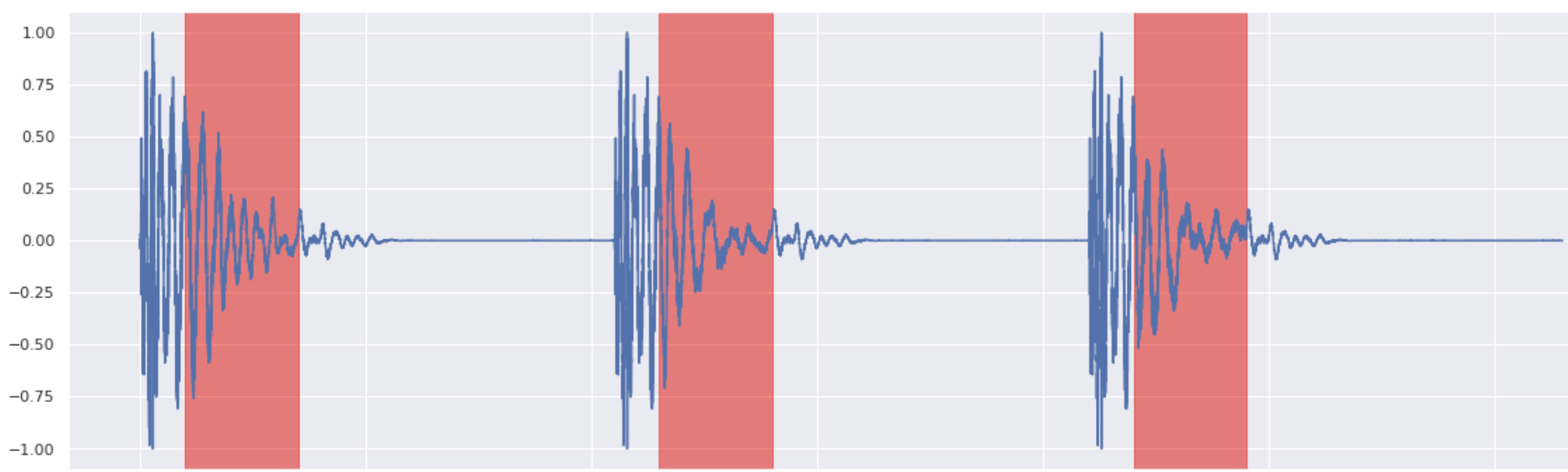
Kick Inpainting 5
Snare Inpainting 1
Snare Inpainting 2
Snare Inpainting 3
Snare Inpainting 4
Obtaining Variations of a Sound by Noising it and Denoising it via SDE
Let’s take a sound x(0) of the test set. We can noise it at a t level (associated to a value of σ): \[ \mathbb{x}(t) = m(t) \mathbb{x}(0) + \sigma(t) \epsilon \] where Ɛ is an isotropic Gaussian
Then, we perform SDE denoising from t to 0 and we obtain variations of the sound.
The more σ is big, the more the variations are diverse.
Cymbal Variations
The original:
For σ=0.1 and a VP schedule.
All in a row:
Snare Variations
The original:
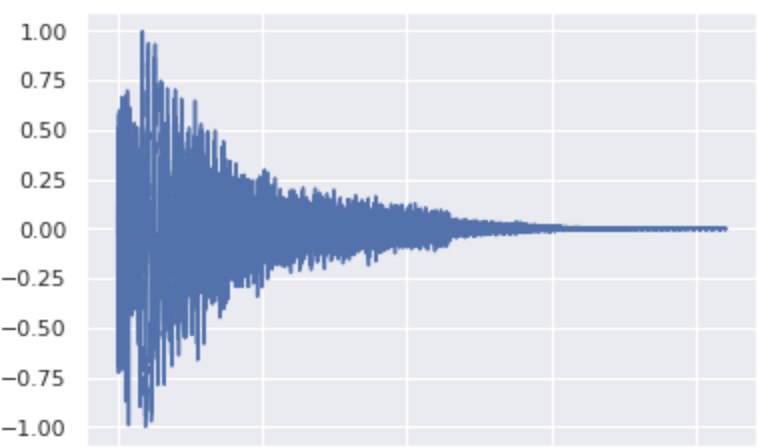
For σ=0.1 and a VP schedule.
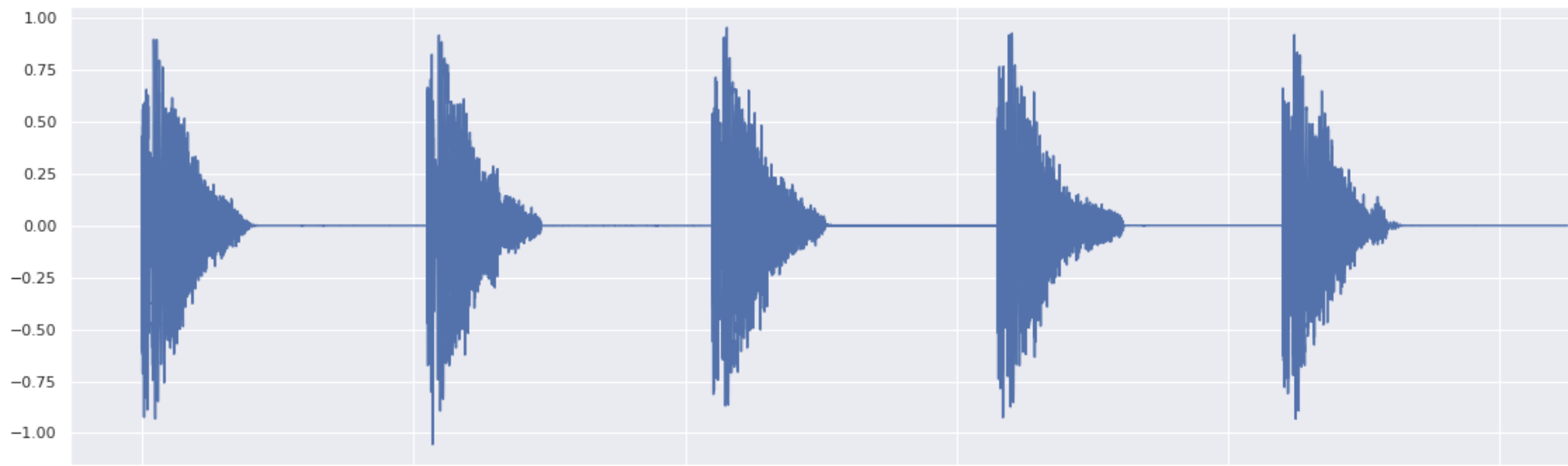
All in a row:
For σ=0.2 and a VP schedule.
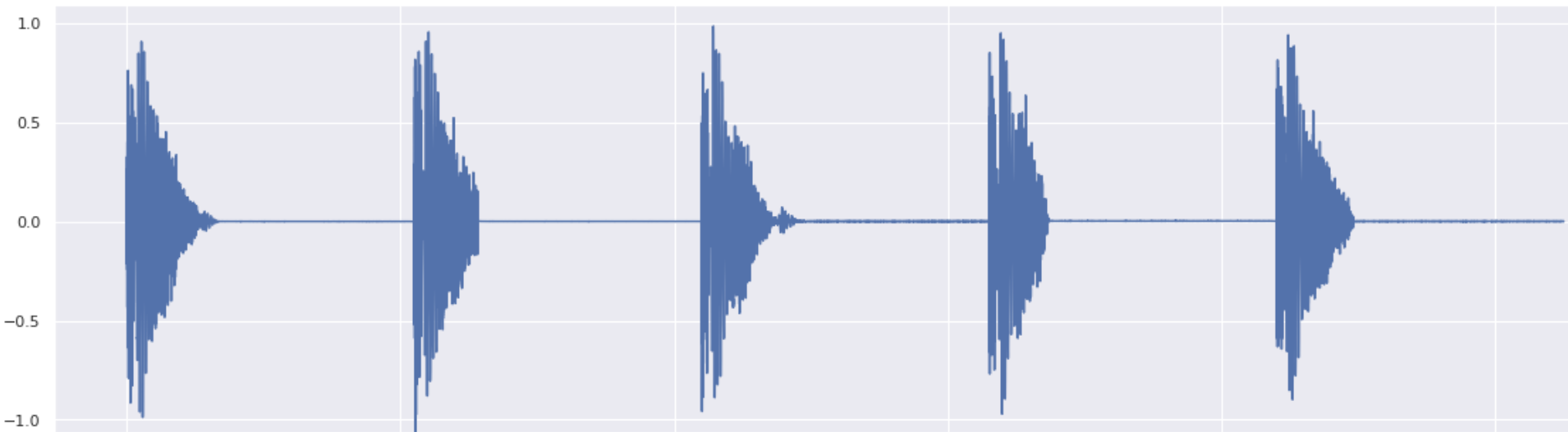
All in a row:
For σ=0.4 and a VP schedule.
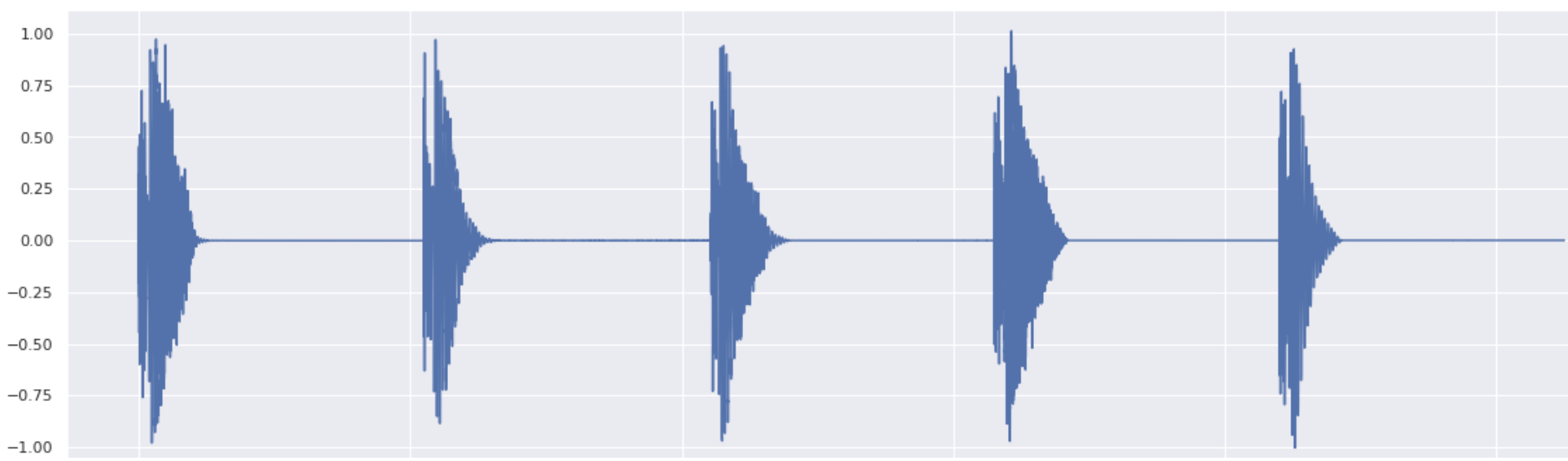
All in a row:
For σ=0.7 and a VP schedule.

All in a row:
Class-Conditioning and Class-Mixing with a Classifier via ODE
We separately trained a noise-conditioned classifier to recognize the class of a sound at different noise levels σ. Then we can generate sounds from only one class and even mix them !
For instance, this is a cymbal from the test set:
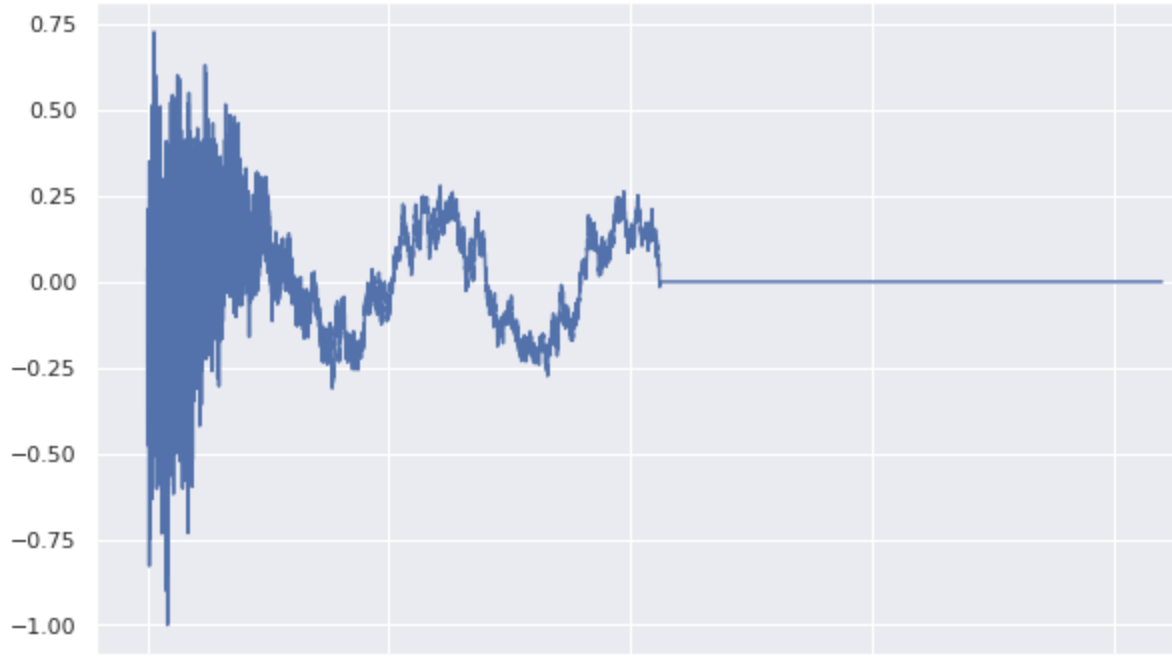
When we use the forward ODE to obtain its latent representation and do the backward ODE with a kick-class constraint, we obtain a “kicky” version of it:
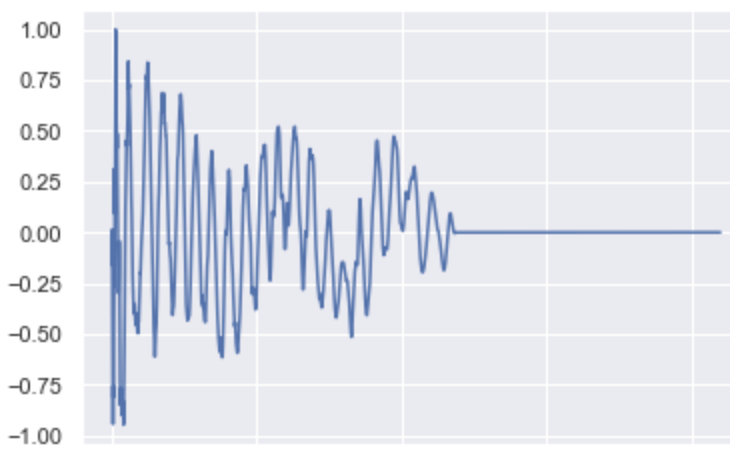
Now, here are the kick, snare and cymbal versions when running backward the constrained ODE starting from a random noise:
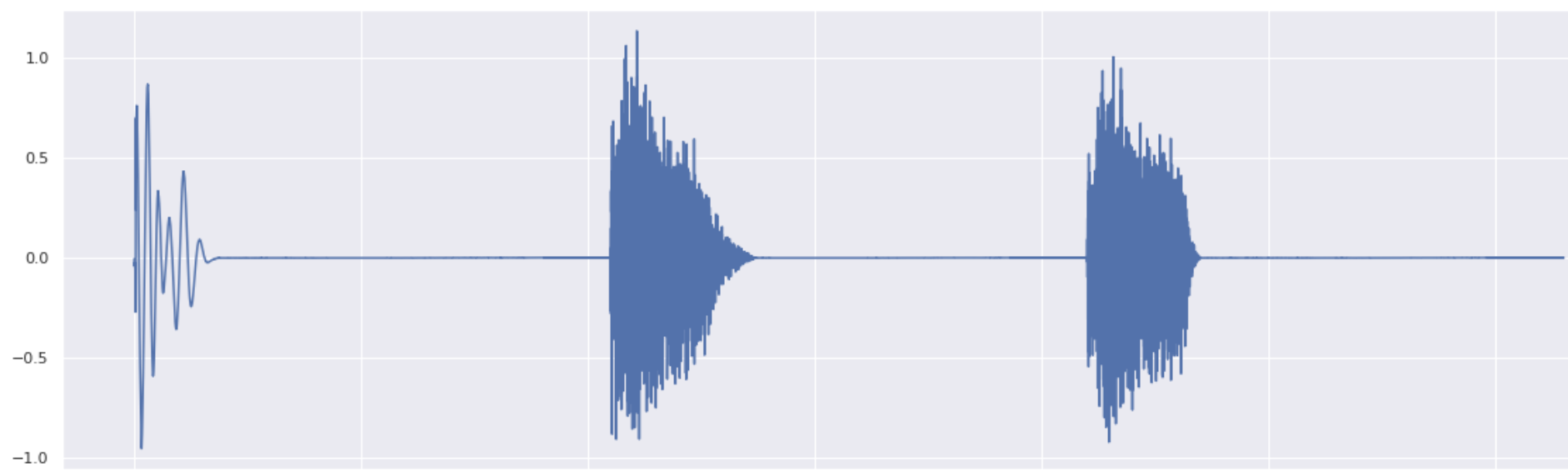
Here are the results of the class-mixing, with different weightings:
\[ \lambda_\text{kick}=0, \lambda_\text{snare}=1, \lambda_\text{cymbal}=0 \]
\[ \lambda_\text{kick}=0.2, \lambda_\text{snare}=0.8, \lambda_\text{cymbal}=0 \]
\[ … \]
\[ \lambda_\text{kick}=1, \lambda_\text{snare}=0, \lambda_\text{cymbal}=0 \]
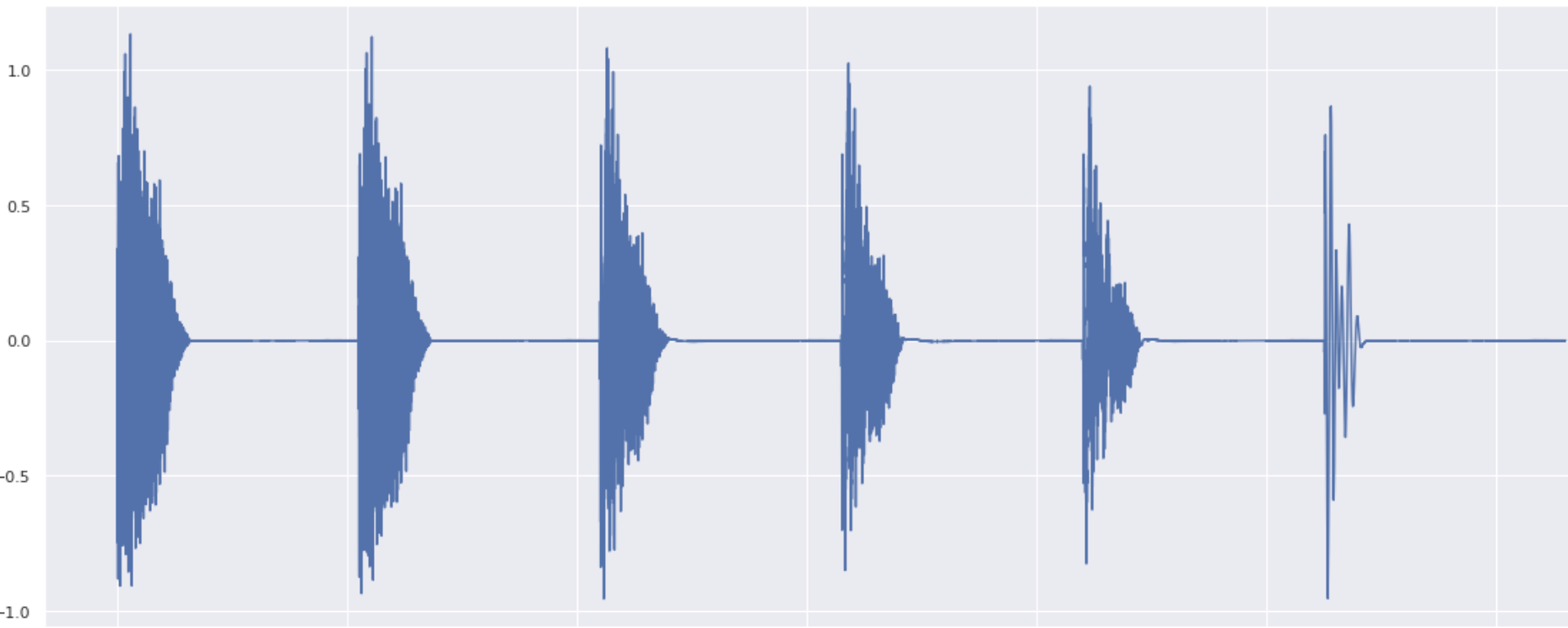
Now, we can operate a more subtle weighting in order to “snarify” a bit the kick:
\[ \lambda_\text{kick}=0.95, \lambda_\text{snare}=0.05, \lambda_\text{cymbal}=0 \]
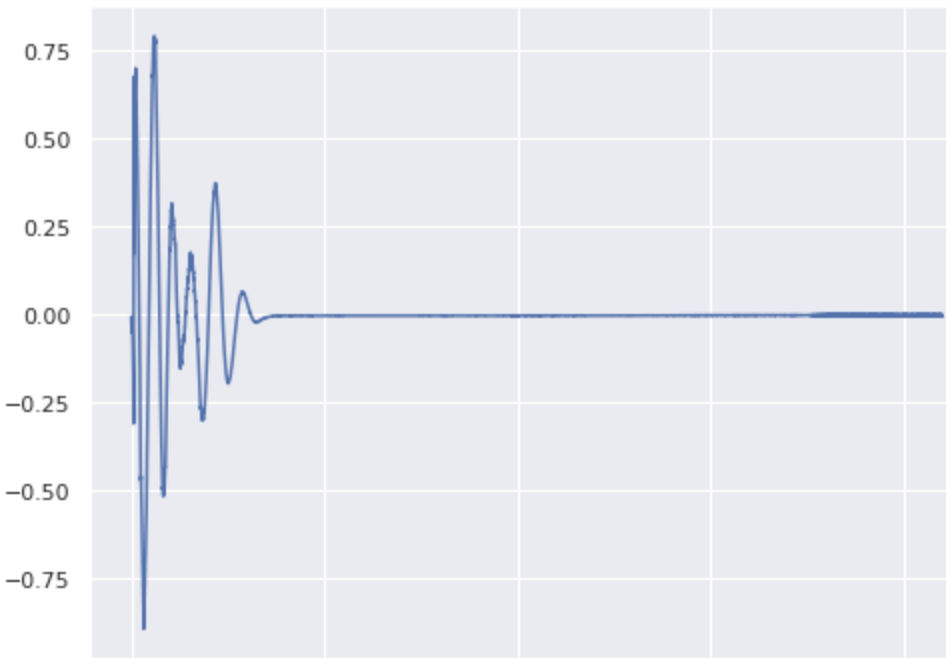
\[ \lambda_\text{kick}=0.9, \lambda_\text{snare}=0.1, \lambda_\text{cymbal}=0 \]
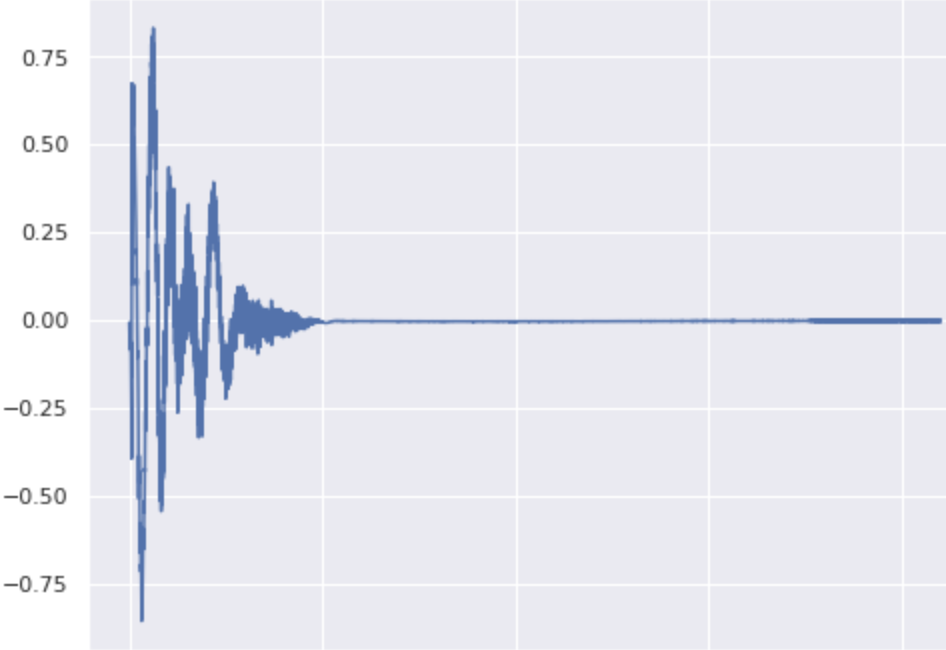
\[ \lambda_\text{kick}=0.85, \lambda_\text{snare}=0.15, \lambda_\text{cymbal}=0 \]
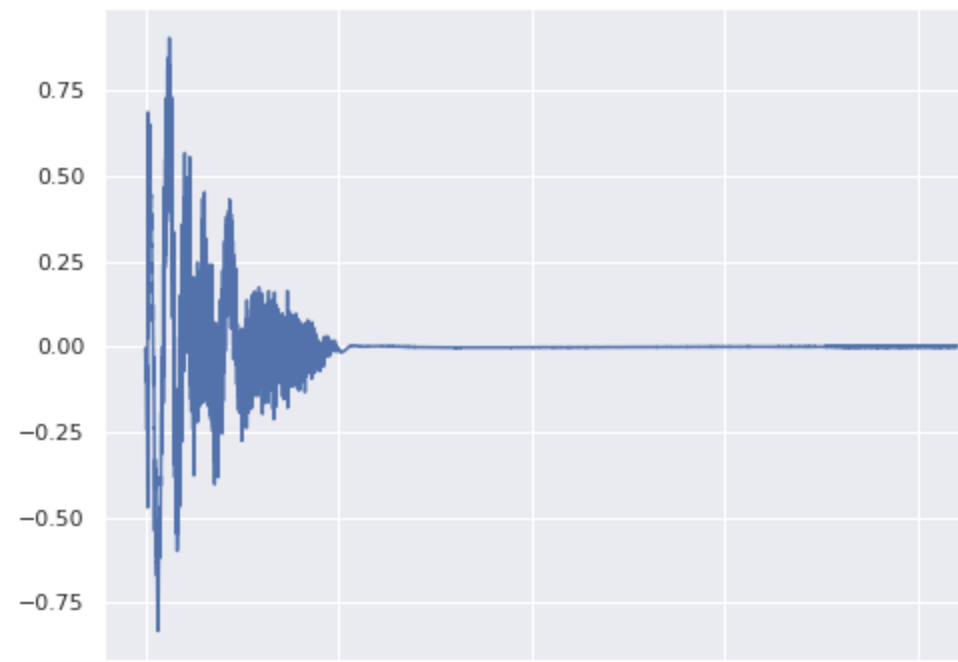
Obtaining Variations of a sound by Noising it and applying Class-Mixing Denoising via SDE
Like in the paragraph “Obtaining Variations of a Sound by Noising it and Denoising it via SDE”, we add noise to our sound: \[ \mathbb{x}(t) = m(t) \mathbb{x}(0) + \sigma(t) \epsilon \]
Then, we denoise it with the class conditional SDE in order to orient the variations of the sound to a particular class or mix of classes:
Cymbal
Original:
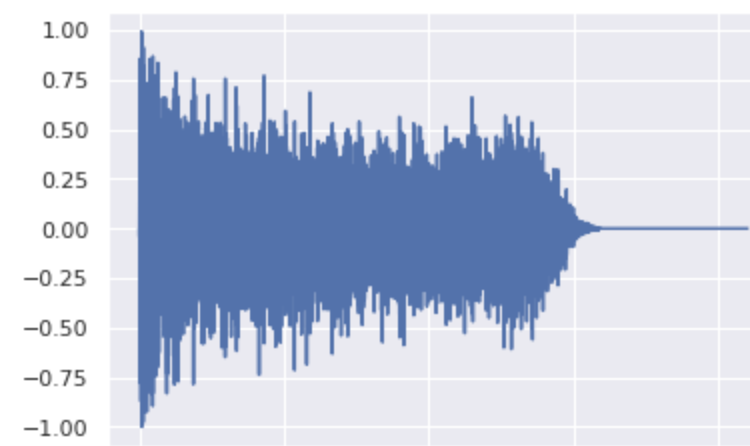
Variations with σ=0.5 in the snare class:
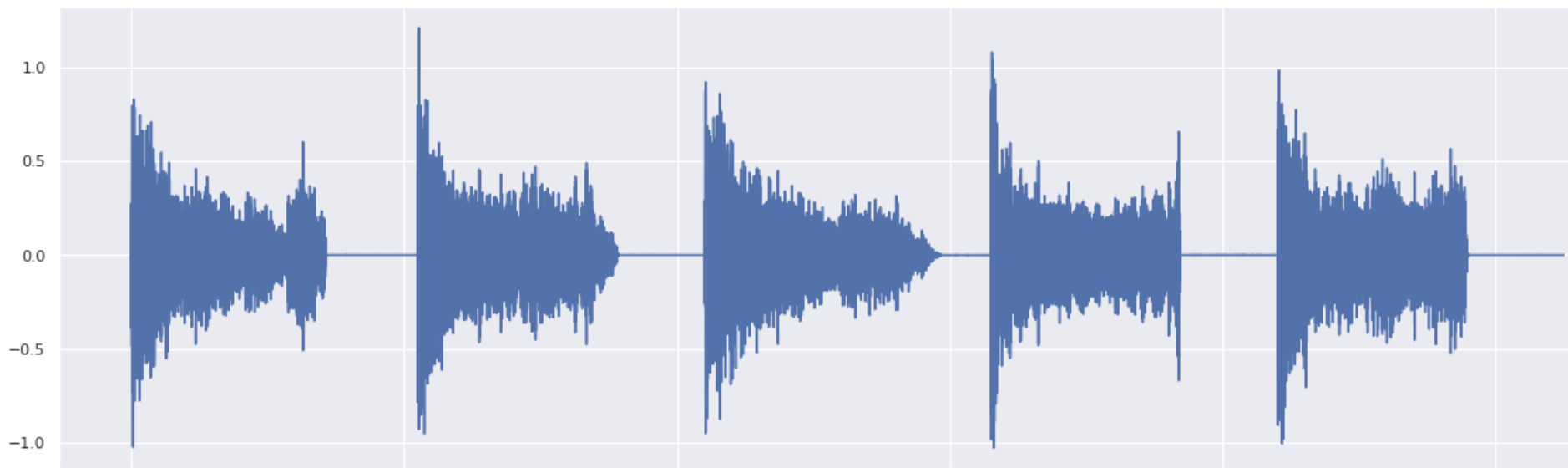
All in a row:
Another variation
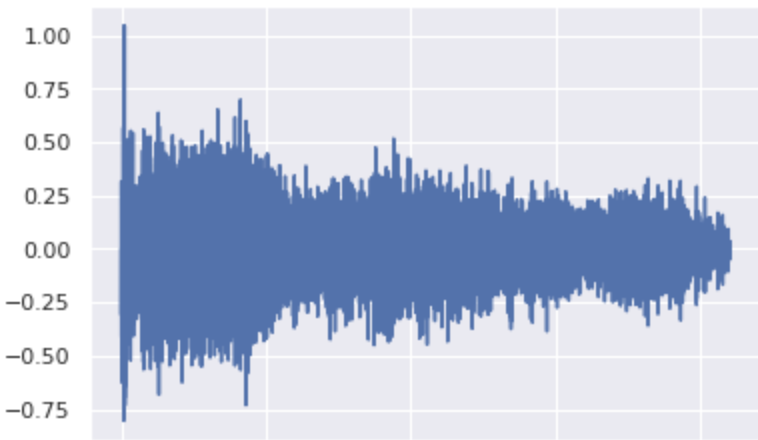
Another with σ=0.6 in the snare class:
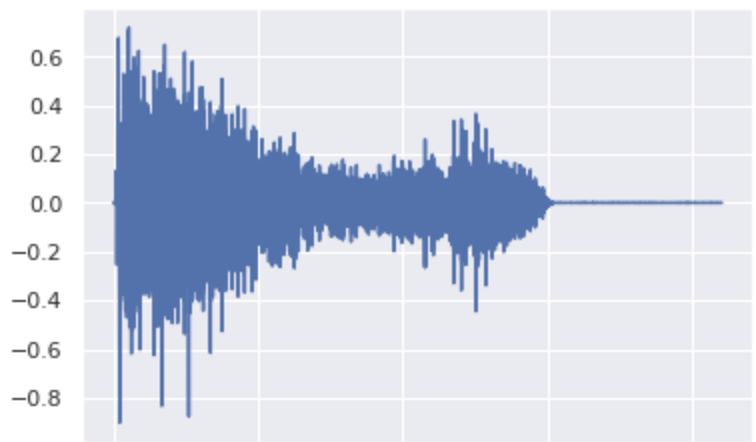
From HiHat to Kick
Original:
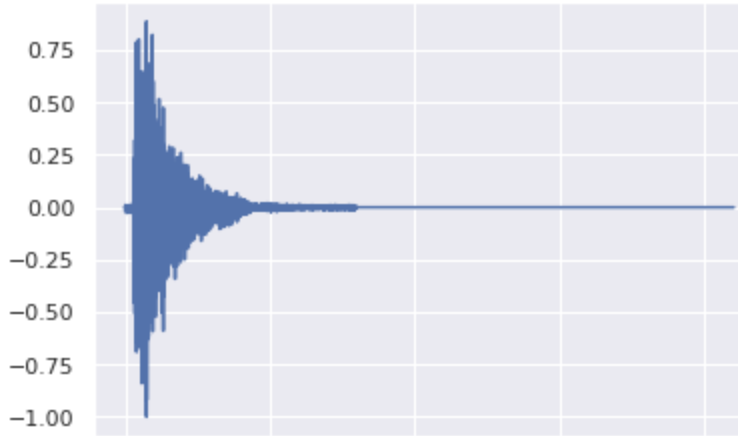
One variation with σ=0.6 in the kick class:
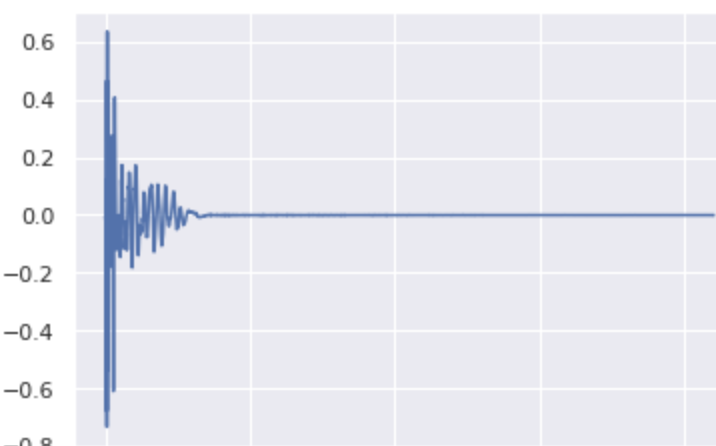
It seems that the model keeps the length, the shape and the percussive aspect of the sound.
From Kick to Snare
Original:
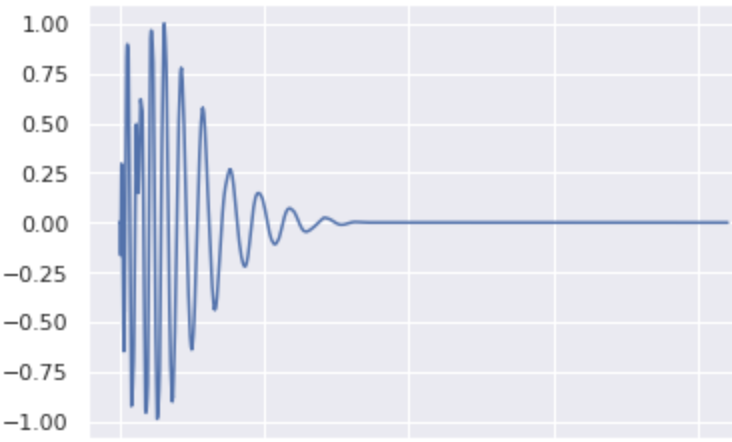
It is difficult to change the class of a kick because of its thin and low frequency waveform even with σ=0.95
When trying to change a kick to a snare, it makes the sound a bit higher
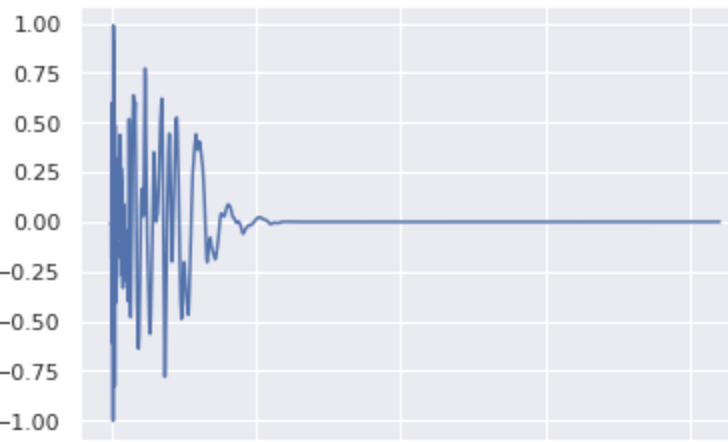
Mixing the classes from a Snare
The Snare is here noised at the level σ=0.8. Then we show the effect of differents weightings of the classes:
Original:
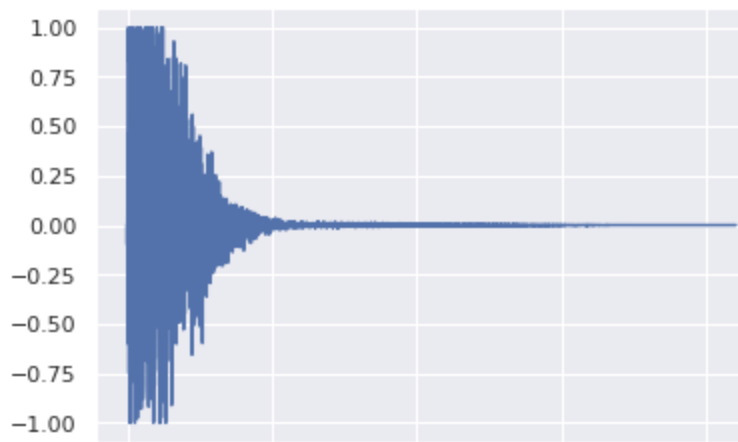
\[ \lambda_\text{kick}=0.0, \lambda_\text{snare}=0.05, \lambda_\text{cymbal}=0.95 \]
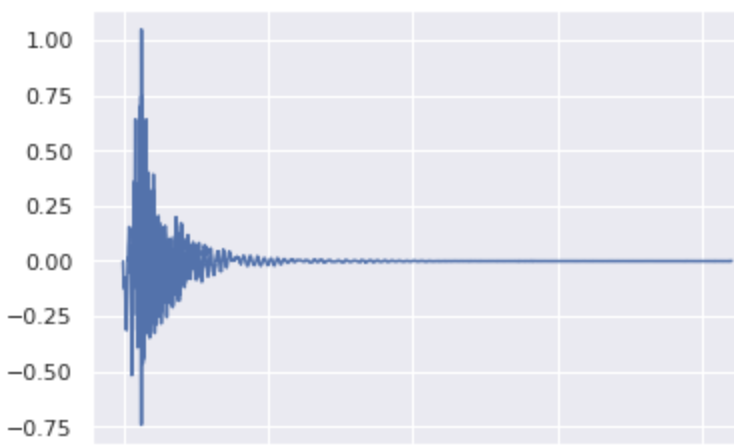
\[ \lambda_\text{kick}=0.8, \lambda_\text{snare}=0.2, \lambda_\text{cymbal}=0 \]
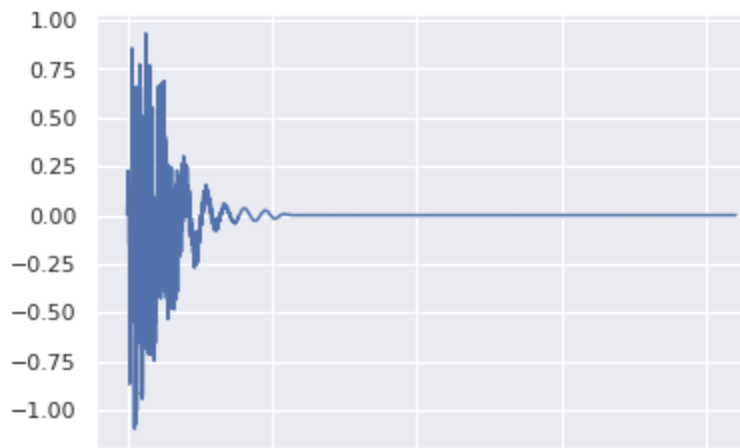
\[ \lambda_\text{kick}=0.5, \lambda_\text{snare}=0.5, \lambda_\text{cymbal}=0 \]